已知：如图，正比例函数y=ax的图象与反比例函数的图象交于点A（3，2）
（1）试确定上述正比例函数和反比例函数的表达式；
（2）根据图象直接回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值；
（3）M（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

某区共有甲、乙、丙三所初中，所有九年级学生参加了一次数学测试．老师们对其中的一道题进行了分析，把每个学生的解答情况归结为下列四类情况之一：A--概念错误；B--计算错误；C--解答基本正确，但不完整；D--解答完全正确．各校出现这四类情况的人数分别占本校九年级学生数的百分比如下表所示：

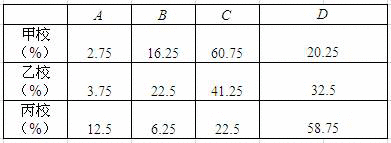
已知甲校九年级有400名学生，这三所学校九年级学生人数的扇形统计图如图所示：

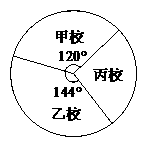
根据以上信息，解答下列问题：
（1）求全区九年级学生总数；
（2）求全区解答完全正确的学生数占全区九年级学生总数的百分比m（精确到0.01%）；
（3）请你对表中三校的数据进行对比分析，给丙校九年级数学老师提一个值得关注的问题，并说明理由．

如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A′C′D′．
（1）证明△A′AD′≌△CC′B；
（2）若∠ACB=30°，试问当点C'在线段AC上的什么位置时，四边形ABC′D′是菱形，并请说明理由．

先化简，再求值：.其中x=-3，y=-2.

四边形ABCD是直角梯形，BC∥AD，∠BAD=90°，BC与y轴相交于点M，且M是BC的中点，A、B、D三点的坐标分别是A（），B（），D（3，0）．连接DM，并把线段DM沿DA方向平移到ON．若抛物线经过点D、M、N．设抛物线与x轴的另一个交点为E，点Q是抛物线的对称轴上的一个动点，当点Q在什么位置时有|QE-QC|最大？并求出最大值．    

（2010重庆改编）等边的两边AB、AC所在直线上分别有两点M、N，D为外一点，且,,BD=DC.探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及的周长Q与等边的周长L的关系．
（I）如图1，当点M、N在边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系是_____________；此时___________；

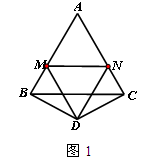
（II）如图2，点M、N在边AB、AC上，且当DMDN时，猜想（I）问的两个结论还成立吗？写出你的猜想并加以证明；

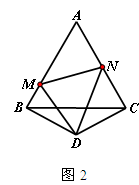
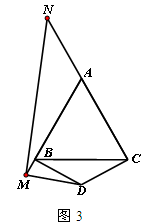
（III）如图3，当M、N分别在边AB、CA的延长线上时，若AN=，则Q=_________（用、L表示）．

如图，等腰梯形ABCD中，AD∥BC，AD=3cm，BC=7cm，∠B=60°，P是底边BC上一点（不和B、C重合），连接AP，过P作PE交DC于E，使得∠APE=∠B．
（1）求证：△ABP∽△PCE；
（2）求AB的长；
（3）在底边BC上是否存在一点P，使得DE:EC=5:3？为什么？

（湖北襄阳）如图，点P是正方形ABCD边AB上一点(不与点A、B重合)，连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE、DF.
（1）求证：∠ADP=∠EPB；
（2）求∠CBE的度数；
（3）当的值等于多少时，△PFD∽△BFP？并说明理由．

如图，已知抛物线经过A（，0），B（）及原点O，顶点为C．（1）求抛物线的解析式；（2）P是抛物线上第一象限内的动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
 

（2009湖南怀化）如图，在直角梯形OABC中，OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．当t为何值时，△PQF是等腰三角形？请写出推理过程．