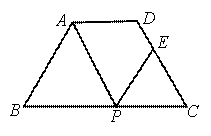
如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P是底边BC上一点(不和B、C重合),连接AP,过P作PE交DC于E,使得∠APE=∠B.
(1)求证:△ABP∽△PCE;
(2)求AB的长;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?为什么?
答案
证明:(1)∵等腰梯形ABCD,∠APE=∠B
∴∠B=∠C=∠APE=60°,
∴∠BAP+∠BPA=120°
∠CPE+∠BPA=120°
∴∠BAP=∠CPE
又∵∠B=∠C
∴△ABP∽△PCE
(2)延长BA,CD交于点F,
∴△FBC是等边三角形
∴FB=FC=BC=7cm,
又∵AD∥BC,
∴△FAD是等边三角形
∴FA=FD=AD=3cm
∴AB=FB-FA=7cm-3cm=4cm

(3)设BP=x,则PC=7-x,
∵CD=4,DE:EC=5:3,
∴EC=4×![]() =
=![]() =1.5,
=1.5,
∵△ABP∽△PCE
∴![]() ,
,
即![]() ,
,
解之得,x=1或6,
即BP=1cm或6cm时,DE:EC=5:3.
知识点:相似三角形的判定与性质
(1)由弦图模型的变形,得△ABP∽△PCE;(2)延长BA,CD构造等边三角形,可得AB的长;(3)利用△ABP∽△PCE,对应边成比例,可求的BP的长.
略








