1编号:3443题型:解答题测试正确率:48.15%
2编号:3306题型:解答题测试正确率:100.0%
3编号:3294题型:解答题测试正确率:40.0%
4编号:3272题型:解答题测试正确率:88.62%
5编号:3271题型:解答题测试正确率:91.45%
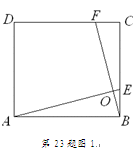
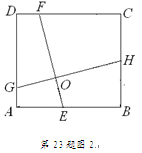
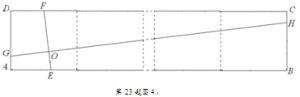
(2010年浙江绍兴市)(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.(2)如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.求GH的长.(3)已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.直接写出下列两题的答案:①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

6编号:3175题型:解答题测试正确率:0%
7编号:3167题型:解答题测试正确率:44.44%
8编号:3114题型:解答题测试正确率:36.0%
如图,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.(1)求梯形ABCD的周长;(2)动点P从点B出发,以1cm/s的速度沿B→A→D→C方向向点C运动;动点Q从点C出发,以1cm/s的速度沿C→D→A方向向点A运动;过点Q作QF⊥BC于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之结束,设运动时间为t秒.问:①当点P在B→A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由.②在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.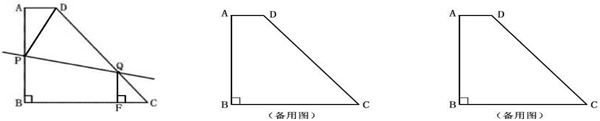
9编号:3113题型:解答题测试正确率:75.73%
10编号:2997题型:解答题测试正确率:43.24%