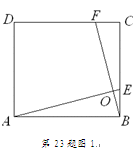
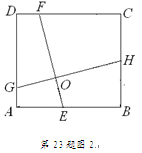
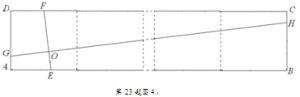
(2010年浙江绍兴市)(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.(2)如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.求GH的长.(3)已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.直接写出下列两题的答案:①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

答案
(1)证明:如图1,∵四边形ABCD为正方形,第23题图1∴AB=BC,∠ABC=∠BCD=90°,∴∠EAB+∠AEB=90°.∵∠EOB=∠AOF=90°,∴∠FBC+∠AEB=90°,∴∠EAB=∠FBC,∴△ABE≌△BCF,∴BE=CF.(2)解:如图2,过点A作AM//GH交BC于M,过点B作BN//EF交CD于N,AM与BN交于点O/,则四边形AMHG和四边形BNFE均为平行四边形,第23题图2O′NM∴EF=BN,GH=AM,∵∠FOH=90°,AM//GH,EF//BN,∴∠NO/A=90°,故由(1)得,△ABM≌△BCN,∴AM=BN,∴GH=EF=4.(3)①8.②4n.
知识点:全等三角形的判定与性质 正方形的性质 相似三角形的判定与性质
(1)研究基本图形(2)需求目标图形(3)寻求解决问题的策略
(1)第一二问问题不大,如何有第二问推到到第三问上;(2)找到目标图形,利用相似比例来解决问题











