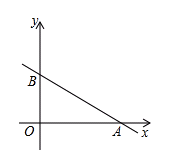（2011云南曲靖）如图：直线y=kx＋3与x轴、y轴分别交于A、B两点，tan∠OAB= $\frac{3}{4}$ ,点C(x,y)是直线y=kx+3上与A、B不重合的动点.（1）求直线y=kx+3的解析式；（2）当点C运动到什么位置时△AOC的面积是6；（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由.

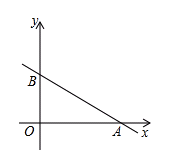
答案

解：（1）∵直线y＝kx＋3与y轴分别交于B点，
∴B（0，3），
∵tan∠OAB＝ $\frac{3}{4}$ ，
∴OA＝4，∴A（4，0），
∵直线y＝kx＋3过A（4，0），
∴4k＋3＝0，k＝－ $\frac{3}{4}$ ，
∴直线的解析式为：y＝－ $\frac{3}{4}$ x＋3；
（2）∵A（4，0），
∴AO＝4，
∵△AOC的面积是6，
∴△AOC的高为3，
∴C点的纵坐标为 $\pm$ 3，
∵直线的解析式为：y＝－ $\frac{3}{4}$ x＋3，代入求得x＝0或x＝8，
∴C的坐标为(0,3)或(8,-3)
∵C与B不重合，
∴当C运动到(8,-3)时，△AOC的面积是6；
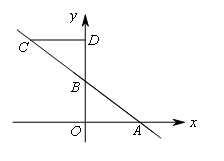
（3）当过点C的另一直线CD与y轴相交于D点，且CD⊥y轴于点D时，BD＝BO＝3，△BCD与△AOB全等，
∴C点纵坐标为6，
∴6＝－ $\frac{3}{4}$ x＋3，解得：x＝－4，
∴C点坐标为：（－4，6）．

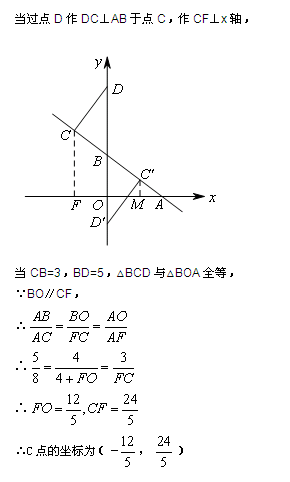
知识点：三角形全等性质与判定三角形全等性质与判定运动变化型问题运动变化型问题

本次重点问题在第三问，容易出现找不全的情况，所以针对这些情况，要找到突破口；（1）先对C进行分类讨论，因为只要C的位置确定，三角形的分类才确定；（2）三角形分类时重点抓住角，从角然后到边，确保不重不漏。

略

下载次数：8

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>