如图所示，四边形OABC是矩形，点A、C的坐标分别为(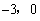)，(0，1)，点D是线段BC上的动点(与端点B、C不重合)，过点D作直线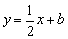交折线OAB于点E.(1)记△ODE的面积为S．求S与b的函数关系式；(2)当点E在线段OA上时，且tan∠DEO=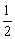.若矩形OABC关于直线DE的对称图形为四边形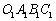．试探究四边形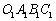与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.

答案

解：（1）∵四边形OABC是矩形，点A、C的坐标分别为（﹣3，0），（0，1），
∴B（﹣3，1），若直线经过点A（﹣3，0）时，则b=，若直线经过点B（﹣3，1）时，则b=，若直线经过点C（0，1）时，则b=1，
①若直线与折线OAB的交点在OA上时，即1＜b≤，如图1，此时E（2b，0），
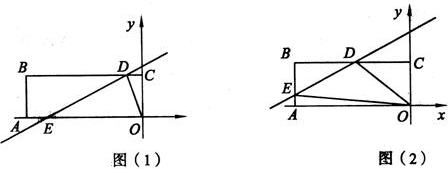
∴S=OE•CO=×2b×1=b；②若直线与折线OAB的交点在BA上时，即＜b＜，如图2此时E（﹣3，），D（2b﹣2，1），
∴S=S_矩﹣（S_△_OCD+S_△_OAE+S_△_DBE）=3﹣[（2b﹣2）×1+×（5﹣2b）•（﹣b）+×3（b﹣）]=b﹣b²，
∴S=； $\begin{cases} b (b\leq \frac{3}{2})\\ \frac{5}{2}b-b^{2} (\frac{3}{2}<b<\frac{5}{2}) \end{cases}$

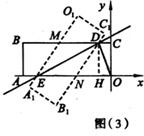
（2）如图3，设O₁A₁与CB相交于点M，OA与C₁B₁相交于点N，则矩形O₁A₁B₁C₁与矩形OABC的重叠部分的面积即为四边形DNEM的面积．由题意知，DM∥NE，DN∥ME，∴四边形DNEM为平行四边形，根据轴对称知，∠MED=∠NED，又∠MDE=∠NED，
∴∠MED=∠MDE，∴MD=ME，∴平行四边形DNEM为菱形．过点D作DH⊥OA，垂足为H，由题易知，=，DH=1，∴HE=2，
设菱形DNEM的边长为a，则在Rt△DHN中，由勾股定理知：a²=（2﹣a）²+1²，∴a=，∴S_四边形_DNEM=NE•DH=．∴矩形OA₁B₁C₁与矩形OABC的重叠部分的面积不发生变化，面积始终为．