（2010年浙江省东阳县）如图，P为正方形ABCD的对称中心，A（0，3），B（1，0），直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以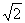个单位每秒速度运动，运动时间为t。求：（1）C的坐标为；（2）当t为何值时，△ANO与△DMR相似？（3）△HCR面积S与t的函数关系式；并求以A、B、C、R为顶点的四边形是梯形时t的值及S的最大值。

答案

（1）C（4，1）（2）当∠MDR＝45^０时，t＝2,点H（2，0）当∠DRM＝45^０时，t＝3,点H（3，0）（３）S＝－ｔ^２＋２ｔ（０＜ｔ≤４）；S＝ｔ^２－２ｔ（ｔ＞４）当CR∥AB时，ｔ＝，Ｓ＝当AR∥BC时，ｔ＝，Ｓ＝当BR∥AC时，ｔ＝，Ｓ＝

（1）动点先研究基本图形；(2)研究动点的五个量；（3）表达线段（4）找几何特征（相似需要分类讨论，面积问题先找状态拐点，梯形先满足一组边平行）

（1）两个点运动，把握不住图形的特征；（2）是否需要分类讨论？点在什么位置需要分类讨论？

下载次数：1