如图，将边长为的正方形ABCD沿对角线AC平移，使点A移至线段AC的中点A＇处，得新正方形A＇B＇C＇D＇，新正方形与原正方形重叠部分（图中阴影部分）的面积是（）

如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG.

（1）求证：①DE=DG；②DE⊥DG；
（2）尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
（3）连接（2）中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；
（4）当时，请直接写出的值.

如图，已知AD为△ABC的角平分线，AB＜AC，在AC上截取CE=AB，M、N分别为BC、AE的中点，求证MN‖AD.

如图，P是y轴上一动点，是否存在平行于y轴的直线x=t，使它与直线y=x和直线y=x+2分别交于点D、E（E在D的上方），且△PDE为等腰直角三角形？若存在，求t的值及点P的坐标；若不存在，请说明原因．

兄弟两人骑马进城，全程51千米。马每小时行12千米，但只能一个人骑马。哥哥每小时步行5千米，弟弟每小时行4千米。两人轮换骑马和步行，骑马者走过一段距离就下鞍栓马（时间忽略不计）然后独自步行;而步行者到达此地，再上马前进。如果他们早晨六点动身，何时能同时到达城里？

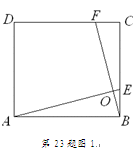
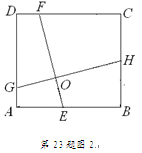
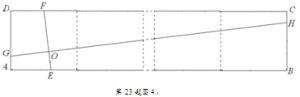
(2010年浙江绍兴市)（1）如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.（2）如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH＝90°,EF＝4.求GH的长.（3）已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,∠FOH＝90°,EF＝4.直接写出下列两题的答案：①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).

（2011浙江温州）如图，O是正方形ABCD的对角线BD上一点，⊙O与边AB，BC都相切，点E，F分别在边AD，DC上．现将△DEF对折，折痕EF与⊙O相切，此时点D恰好落在圆心O处，若DE=2，则正方形ABCD的边长是（    ）

如图，正方形纸片ABCD的边长为1，M、N分别是AD、BC边上的点，将纸片的一角沿过点B的直线折叠，使A落在MN上，落点记为A′，折痕交AD于点E,若M、N分别是AD、BC边的中点，则A′N=　　　　　　　　;若M、N分别是AD、BC边的上距DC最近的n等分点（n≥2,且n为整数），则A′N=　　　　　　　　　　.（用含有n的式子表示）

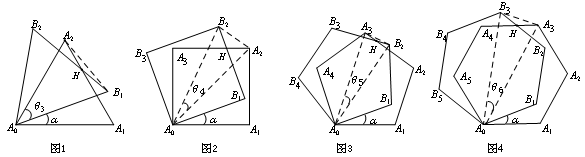
（2010江西）课题：两个重叠的正多边型，其中一个绕某一顶点旋转所形成的有关问题。实验与论证设旋转角∠A₁A₀B₁=α（α1A₀A₂）,θ₃，θ₄，θ₅，θ₆，所表示的角如图所示。
（1）用含α的式子表示角的度数：θ₃=　　　　　　　　　　_θ₄=　　　　　　　　　　　θ₅=_________
　　　　　　　　
（2）图1－图4中，连接A₀H时，在不添加其他辅助线的情况下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请选择期中的一个图给出证明；若不存在，请说明理由；归纳与猜想设正n边形A₀A₁A₂…A_n－1与正n边形A₀B₁B₂…B_n－1重合（其中，A₁与B₁重合），现将正n边形A₀B₁B₂…B_n－1绕顶点A₀逆时针旋转α（）．
（3）设θ_n与上述“θ₃，θ₄，…”的意义一样，请直接写出θ_n的度数；（4）试猜想在正n边形的情形下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请将这条线段用相应的顶点字母表示出来（不要求证明）；若不存在，请说明理由．

（2011绥化）在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G连接EG，CG，如图1，易证EG=CG且EG⊥CG.
（1）将△BEF绕点B逆时针旋转90°，如图2，则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．
（2）将△BEF绕点B逆时针旋转180°，如图3，则线段EG和CG有怎样的数量关系和位置关系？请写出你的猜想.并加以证明．