如图，四边形ABCD是正方形，点E，K分别在BC，AB上，点G在BA的延长线上，且CE=BK=AG.
（1）求证：①DE=DG；②DE⊥DG；
（2）尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；
（3）连接（2）中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；
（4）当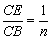
时，请直接写出
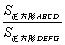的值.
的值.答案
（1）证明：∵四边形ABCD是正方形，∴DC=DA，∠DCE=∠DAG=90°．又∵CE=AG，∴△DCE≌△DAG，∴DE=DG，∠EDC=∠GDA，又∵∠ADE+∠EDC=90°，∴∠ADE+∠GDA=90°∴DE⊥DG．
（2）略
（3）四边形CEFK为平行四边形．证明：设CK、DE相交于M点，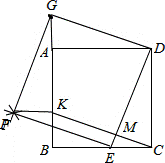
∵四边形ABCD和四边形DEFG都是正方形，∴AB∥CD，AB=CD，EF=DG，EF∥DG，∵BK=AG，∴KG=AB=CD，∴四边形CKGD是平行四边形，∴CK=DG=EF，CK∥DG，∴∠KME=∠GDE=∠DEF=90°，∴∠KME+∠DEF=180°，∴CK∥EF，∴四边形CEFK为平行四边形．
（4）∵
，∴设CE=x，CB=nx，∴CD=nx，∴DE2=CE2+CD2=n2x2+x2=（n2+1）x2，∵BC2=n2x2，∴
．
（1）由已知证明DE、DG所在的三角形全等，即△DCE≌△DAG，得到对应角相等，再通过等量代换证明DE⊥DG；
（2）根据正方形的性质分别以点G、E为圆心以DG为半径画弧交点F，得到正方形DEFG；
（3）由已知首先证四边形CKGD是平行四边形，然后证明四边形CEFK为平行四边形；
（4）都是正方形，所以只需找出边长平方之比就可以了．
略
WORD格式（
