如图,直线l过正方形ABCD的顶点B,AB=BC,∠ABC=90°,AE⊥l,CF⊥l,垂足分别为E、F,试判断EF、AE、CF有怎样的数量关系,并说明理由.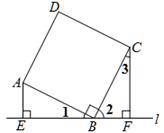

解:EF=AE+CF,理由如下:
∵∠ABC=90°
∴__________=90°
∵AE⊥l,CF⊥l,
∴∠AEB=∠BFC=90°
∴___________=90°
∴∠1=∠3
在△AEB和△BFC中
_________________
∴______________
∴AE=________,BE=________
∴EF=BE+BF=CF+AE
①∠1+∠2,
②∠2+∠3,
③∠2=∠3,
④,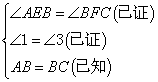
⑤,
⑥△AEB≌△BFC(ASA),
⑦△AEB≌△BFC(AAS),
⑧BF,
⑨CF.
以上空缺处依次填写正确的顺序为()

如图,CB⊥AE于B,AF交CB于D,交CE于F,若DB=EB,AD=CE,试判断AF和CE有怎样的位置关系,并说明理由.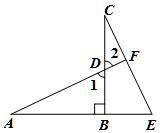

解:AF⊥CE,理由如下:
∵CB⊥AE
∴∠ABD=∠CBE=90°
∴∠1+∠A=90°
在Rt△ABD和Rt△CBE中
__________________
∴________________
∴∠A=∠C
∵∠1=∠2
∴______________=90°
∴_______________
即AF⊥CE
①,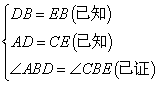
②,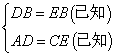
③△ABD≌△CBE(SAS),
④Rt△ABD≌Rt△CBE(HL),
⑤∠2+∠C=90°,
⑥∠1+∠A=90°,
⑦∠DFC=90°.
以上空缺处依次填写正确的顺序为()

已知:如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于E,交CD于点F.若AF平分∠CAD,线段FB和FC相等吗?请说明理由.

解:FB=FC,理由如下:
∵∠ADC=90°,BE⊥AC于E
∴∠FDB=∠FEC=90°
∴∠1+∠C=∠2+∠B=90°
∵∠1=∠2
∴________________
∵AF平分∠CAD
∴_______________
在△AFC和△AFB中
___________________
∴_________________
∴FB=FC
①,
②,
③∠3=∠4,
④,
⑤,
⑥△ACF≌△AFB(AAS),
⑦△ACF≌△AFB(ASA).
以上空缺处依次填写正确的顺序为()

已知:如图,点A,F,E,B在一条直线上,AF=BE,AD∥BC,AD=BC,请你判断CF和DE有怎样的位置关系,并说明理由.

解:CF∥DE,理由如下:
∵AF=BE
∴AF+EF=BE+EF
即AE=FB
又∵AD∥BC
∴____________
在△ADE和△BCF中
______________
∴______________
∴_______________(三角形全等,对应角相等)
∴CF∥DE
①,
②,
③,
④,
⑤△ADE≌△BCF(SSA),
⑥△ADE≌△BCF(SAS).
以上空缺处依次填写正确的顺序为()

如图,CB⊥AE于B,AF交CB于D,交CE于F,若DB=EB,AD=CE,证明:Rt△ABD≌Rt△CBE.

证明:∵CB⊥AE
∴∠ABD=∠CBE=90°
在Rt△ABD和Rt△CBE中
_____________________
∴___________________
①,
②,
③△ABD≌△CBE(SAS),
④Rt△ABD≌Rt△CBE(HL),
⑤△ABD≌△BCE(SAS).
以上空缺处依次填写正确的顺序为()

已知:如图,AB=CD,AB∥CD,DE⊥AC,BF⊥AC,垂足分别是E,F.试证明:△DEC≌△BFA

证明:∵DE⊥AC,BF⊥AC
∴∠DEC=∠BFA=90°
∵AB∥CD
∴___________
在△DEC和△BFA中
_______________
∴_______________
①∠C=∠A,
②∠D=∠B,
③,
④,
⑤△DEC≌△BFA(ASA),
⑥△DEC≌△BFA(AAS).
以上空缺处依次填写正确的顺序为()

已知:如图,在Rt△ACD中,∠ADC=90°,BE⊥AC于E,交CD于点F.若AF平分∠CAD,证明:△AFC≌△AFB

证明:∵∠ADC=90°,BE⊥AC于E
∴∠FDB=∠FEC=90°
∴∠1+∠C=∠2+∠B=90°
∵∠1=∠2
∴_________________
∵AF平分∠CAD
∴________________
在△AFC和△AFB中
________________
∴______________
①,
②,
③∠3=∠4,
④,
⑤,
⑥△AFC≌△AFB(AAS),
⑦△AFC≌△AFB(ASA).
以上空缺处依次填写正确的顺序为()

已知:如图,点A,F,E,B在一条直线上,AF=BE,AD∥BC,AD=BC,证明:△ADE≌△BCF.

证明:∵AF=BE
∴AF+EF=BE+EF
即AE=FB
又∵AD∥BC
∴____________
在△ADE和△BCF中
 
_______________
∴_____________
①,
②,
③,
④,
⑤△ADE≌△BCF(SSA),
⑥△ADE≌△BCF(SAS).
以上空缺处依次填写正确的顺序为()

如图,直线l过正方形ABCD的顶点B,AB=BC,∠ABC=90°,AE⊥l,CF⊥l,垂足分别为E、F,求证:△AEB≌△BFC.

证明:∵∠ABC=90°
∴_________=90°
∵AE⊥l,CF⊥l,
∴∠AEB=∠BFC=90°
∴__________=90°
∴∠1=∠3
在△AEB和△BFC中
_______________
∴_____________
①∠1+∠2,
②∠2+∠3,
③∠2=∠3,
④,
⑤,
⑥△AEB≌△BFC(ASA),
⑦△AEB≌△BFC(AAS),.
以上空缺处依次填写正确的顺序为()

已知:如图,B,E,C,F在一条直线上,AB∥DE,∠A=∠D,BE=CF.证明△ABC≌△DEF.

证明:∵AB∥DE
∴_______________
∵BE=CF
∴BE+EC=CF+EC
即BC=EF
在△ABC和△DEF中
_________________
∴_______________
①∠B=∠1,
②∠B=∠E,
③,
④,
⑤△ABC≌△DEF(AAS),
⑥△ABC≌△EDF(AAS).
以上空缺处依次填写正确的顺序为()