如图,CB⊥AE于B,AF交CB于D,交CE于F,若DB=EB,AD=CE,试判断AF和CE有怎样的位置关系,并说明理由.
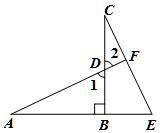
解:AF⊥CE,理由如下:
∵CB⊥AE
∴∠ABD=∠CBE=90°
∴∠1+∠A=90°
在Rt△ABD和Rt△CBE中
__________________
∴________________
∴∠A=∠C
∵∠1=∠2
∴______________=90°
∴_______________
即AF⊥CE
①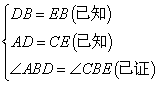 ,
,
②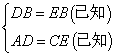 ,
,
③△ABD≌△CBE(SAS),
④Rt△ABD≌Rt△CBE(HL),
⑤∠2+∠C=90°,
⑥∠1+∠A=90°,
⑦∠DFC=90°.
以上空缺处依次填写正确的顺序为()
- A.①③⑤⑦
- B.①③⑥⑦
- C.②④⑤⑦
- D.②④⑥⑦
答案
正确答案:C
略
略








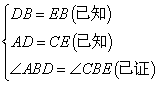 ,
,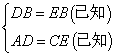 ,
,