如图,直线l过正方形ABCD的顶点B,AB=BC,∠ABC=90°,AE⊥l,CF⊥l,垂足分别为E、F,试判断EF、AE、CF有怎样的数量关系,并说明理由.

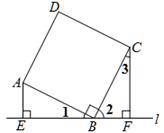
解:EF=AE+CF,理由如下:
∵∠ABC=90°
∴__________=90°
∵AE⊥l,CF⊥l,
∴∠AEB=∠BFC=90°
∴___________=90°
∴∠1=∠3
在△AEB和△BFC中
_________________
∴______________
∴AE=________,BE=________
∴EF=BE+BF=CF+AE
①∠1+∠2,
②∠2+∠3,
③∠2=∠3,
④,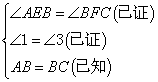
⑤,
⑥△AEB≌△BFC(ASA),
⑦△AEB≌△BFC(AAS),
⑧BF,
⑨CF.
以上空缺处依次填写正确的顺序为()

• A.①②④⑦⑧⑨
• B.①②④⑦⑨⑧
• C.①②⑤⑥⑧⑨
• D.①②⑤⑥⑨⑧

答案

正确答案：A

略

略

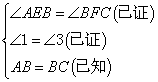下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>