（湖北襄阳）如图，点P是正方形ABCD边AB上一点(不与点A、B重合)，连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE、DF.
（1）求证：∠ADP=∠EPB；
（2）求∠CBE的度数；
（3）当的值等于多少时，△PFD∽△BFP？并说明理由．

如图，已知抛物线经过A（，0），B（）及原点O，顶点为C．（1）求抛物线的解析式；（2）P是抛物线上第一象限内的动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．
 

（2009湖南怀化）如图，在直角梯形OABC中，OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．当t为何值时，△PQF是等腰三角形？请写出推理过程．
 

我市高新技术开发区的某公司，用480万元购得某种产品的生产技术后，并进一步投入资金1520万元购买生产设备，进行该产品的生产加工，已知生产这种产品每件还需成本费40元。经过市场调研发现：该产品的销售单价，需定在100元到300元之间较为合理．当销售单价定为100元时，年销售量为20万件；当销售单价超过100元，但不超过200元时，每件新产品的销售价格每增加10元，年销售量将减少0.8万件；当销售单价超过200元，但不超过300元时，每件产品的销售价格每增加10元，年销售量将减少1万件．设销售单价为x（元），年销售量为y（万件），年获利为w（万元）．（年获利=年销售额-生产成本-投资成本）

（1）直接写出y与x之间的函数关系式；
（2）求第一年的年获利w与x间的函数关系式，并说明投资的第一年，该公司是盈利还是亏损？若盈利，最大利润是多少？若亏损，最少亏损是多少？

抛物线：y＝ax²＋bx＋4与x轴交于点A(－2，0)和B(4，0)、与y轴交于点C．求抛物线的解析式；

若函数y=kx²+2（k+1）x+k-1与x轴只有一个交点，求k的值．

如果关于x的方程kx²-(2k+1)x+(k+2)=0有实数根，求k的取值范围.

孔明是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线的性质时，将一把直角三角板的直角顶点置于平面直角坐标系的原点，两直角边与该抛物线交于、两点，请解答以下问题：
（1）若测得OA=OB=（如图1），求a的值；
（2）对同一条抛物线，孔明将三角板绕点O旋转到如图2所示位置时，过B作BF⊥x轴于点F，测得OF=1，写出此时点B的坐标，并求点A的横坐标；
（3）对该抛物线，孔明将三角板绕点O旋转任意角度时惊奇地发现，交点A、B的连线段总经过一个固定的点，试说明理由并求出该点的坐标．

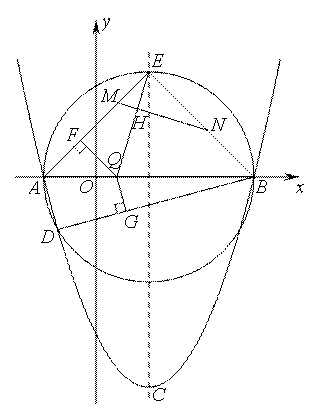
已知抛物线y=ax²+bx+c(a＜0)，顶点C的坐标为（1，-4），且与x轴交于A、B两点，A（-1，0）．
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作圆，与抛物线交于点D，与抛物线的对称轴交于E，依次连接A、D、B、E，点Q为AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断是否为定值，若是，请求出此定值，若不是，请说明理由；
（3）在（2）的条件下，若点H是线段EQ上一点，过点H作MN⊥EQ，MN分别与边AE、BE相交于M、N（M与A、E不重合，N与E、B不重合），请判断是否成立，若成立，请给出证明，若不成立，请说明理由．

如图，Rt△ABC中，AB=8，BC=6，Rt△DBE中，DB=5，BE=7，将两直角三角形直角顶点以及两直角边按如图方式重叠在一起，两斜边交于点P，求点P到AB边的距离是多少？