（2011绥化）在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G连接EG，CG，如图1，易证EG=CG且EG⊥CG.
（1）将△BEF绕点B逆时针旋转90°，如图2，则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．
（2）将△BEF绕点B逆时针旋转180°，如图3，则线段EG和CG有怎样的数量关系和位置关系？请写出你的猜想.并加以证明．

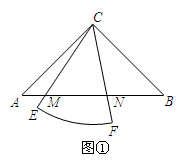
已知Rt△ABC中，∠ACB=90°，CA=CB，有一个圆心角为45°，半径的长等于CA的扇形CEF绕点C旋转，且直线CE，CF分别与直线AB交于点M，N．
（1）当扇形CEF绕点C在∠ACB的内部旋转时，如图①，
求证：MN²=AM²+BN²；
思路点拨：考虑MN²=AM²+BN²符合勾股定理的形式，需转化为在直角三角形中解决．可将△ACM沿直线CE对折，得△DCM，连DN，只需证DN=BN，∠MDN=90°就可以了．
请你完成证明过程：
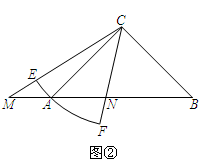
（2）当扇形CEF绕点C旋转至图②的位置时，关系式MN²=AM²+BN²是否仍然成立？若成立，请证明；若不成立，请说明理由．

如图，在△ABC中,∠CAB=70°. 在同一平面内, 将△ABC绕点A旋转到△AB′C′ 的位置, 使得 CC′∥AB, 则∠B′AB = _________

如图，∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于D，AD=2.5cm，DE=1.7cm。则BE的长为（）

如图，已知点C是∠MAN的平分线上一点，CE⊥AB于E，B、D分别在AM、AN上，且AE=（AD+AB）.问：∠1和∠2有何关系？

如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D，AF平分∠CAB交CD于E，交CB于F，且EG∥AB交CB于G，判断CF与GB的大小关系并证明。

如图，△ABC中，∠ABC=60°，AD、CE分别平分∠BAC，∠ACB，判断AC的长与AE+CD的大小关系并证明.

（2011辽宁）在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠DOC=α.将△DOC绕点O按逆时针方向旋转得到△D’OC’（0°＜旋转角＜90°）.连接AC’、BD’，AC’与BD’相交于点M.
（1）当四边形ABCD是矩形时，如图1，请猜想AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想；
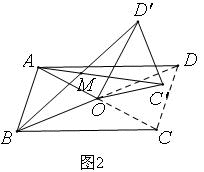
（2）当四边形ABCD是平行四边形时，如图2，已知AC=kBD，请猜想此时AC’与BD’的数量关系以及∠AMB与α的大小关系，并证明你的猜想；
（3）当四边形ABCD是等腰梯形时，如图3，AD∥BC，此时（1）中AC’与BD’的数量关系是否成立？∠AMB与α的大小关系是否成立？不必证明，直接写出结论.

（2011辽宁）如图1，在△ABC中，∠ABC=90°，AB=BC，BD为斜边AC上的中线，将△ABD绕点D顺时针旋转α（0°＜α＜180°），得到△EFD，点A的对应顶点是E，点B的对应顶点是F，连接BE、CF.
（1）判断BE与CF的位置关系、数量关系，并说明理由；
（2）若连接BF、CE，请直接写出在旋转过程中四边形BFEC能形成哪些特殊四边形；
（3）如图2，将△ABC中AB=BC改为AB≠BC时，其他条件不变，直接写出α为多少度时（1）中的两个结论同时成立.

教材12题：如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B´ 处，点A对应点为A´，且B´C=3，求CN和AM的长.