如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB交CD于E,交CB于F,且EG∥AB交CB于G,判断CF与GB的大小关系并证明。
答案
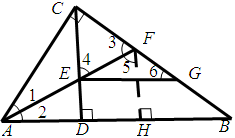
判断:CF=GB
证明:过点F作FH⊥AB于点H,由于AF平分∠CAB,则在△ACF与△AHF中
∴△ACF≌△AHF,则CF=FH,而FH⊥AB,CD⊥AB,∴FH∥CD,从而∠4=∠5,∴∠3=∠4,∴CF=CE,从而CE=FH,又EG∥AB,所以∠6=∠B
∠CEG=∠CDB=90°;则△CEG≌△FHB,∴CG=FB,故CF=BG
找到全等关系是证明的关键
想到将线段转移,想不到全等。








