(2010宁德市)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;
(3)当AM+BM+CM的最小值为  时,求正方形的边长.
时,求正方形的边长.
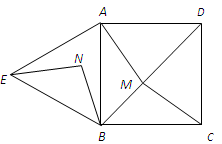
答案
(1)在△AMB与△ENB中
MB=NB
∠NBE=∠MBA
BA=BE
所以△AMB≌△ENB(SAS)
(2))①M在BD的中点时最小,两点之间线段最短。②连接MN,由(1)中可得AM=EN,∠MBN=60°,则△BMN为等边三角形,此时AM+BM+CM=EN+NM+MC,点E、N、M、C在一条直线上时,之和最短,最短只等于EC。所以连接CE交BD于点M,点M即为所求。
(3)做EF⊥CB交CB的延长线于点F,设边长为a,又∠EBF=30°,所以EF=,BF=
,在直角三角形EFC中应用勾股定理可得a=
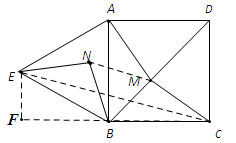
(1)证明三角形全等比较简单;
(2)通过线段之间的等量代换,把一些线段之和转化为两点之间的距离。
(3)通过做辅助线,找到一个既含EC又与正方形的边长有关的直角三角形,进而建立等式求解。
充分利用题目中的已知条件,进行线段之间的转化,把一些线段之和转化为两点之间的距离,利用两点之间线段最短。








