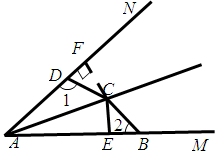
如图，已知点C是∠MAN的平分线上一点，CE⊥AB于E，B、D分别在AM、AN上，且AE=（AD+AB）.问：∠1和∠2有何关系？

答案

解：∠1+∠2=180°
证明：过点C作CF⊥AN于点F，由于AC平分∠NAM，所以CF=CE，则在Rt△ACF和Rt△ACE中
∴△ACF≌△ACE（HL），∴AF=AE，由于2AE=AD+AB，所以AB-AE=AF-AD
∴DF=BE，在△CFD和△CEB中所以△CFD≌△CEB（SAS），∴∠2=∠FDC，又∠1+∠FDC=180°，∴∠1+∠2=180°。

知识点：三角形  全等三角形的性质  全等三角形的判定  

见到角平分线就要想到作垂直，找到全等关系是解决此类问题的关键

找到三角形全等的所有条件

下载次数：1

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>