如图，在△ABC中，AB=AC，
（1）若P为边BC上的中点，连结AP，求证：BP×CP=AB²-AP²；

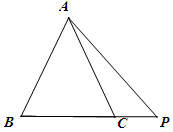
（2）若P是BC边上任意一点，上面的结论还成立吗？若成立请证明，若不成立请说明理由；

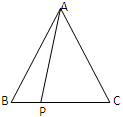
（3）若P是BC边延长线上一点，线段AB、AP、BP、CP之间有什么样的关系？请证明你的结论.

答案

（1）在Rt△ABP中，BP²=AB²-AP²，又BP=CP，所以BP $\times$ CP=AB²-AP²。
（2）结论仍然成立。如图

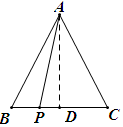
做AD⊥BC于点D，在Rt△ABD中AB²=AD²+BD²在Rt△APD中AP²=AD²+PD²
∴ AB²-AP²=BD²-PD²=(BD-PD)(BD+PD)=PC(PD+BD)=CP $\times$ BP
∴ AP²-AC²=CP $\times$ BP.
（3）如图，

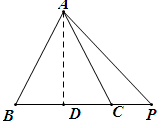
做AD⊥BC于点D，在直角三角形ACD中AC²=AD²+CD²
在直角三角形APD中AP²=AD²+PD²
∴ AP²-AC²=PD²-CD²=(PD-CD)(PD+CD)=PC(PD+BD)=CP $\times$ BP

知识点：等腰三角形的性质勾股定理

通过做辅助线，得到两个直角三角形，分别利用勾股定理，即可。

受第一题的启发，仍然做BC边上高AD，进而出现直角三角形，从而应用勾股定理。

下载次数：2

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>