(2)若将上题中的“正三角形ABC”改为“正方形A₁B₁C₁D₁”(如图),N₁是∠D₁C₁P₁的平分线上一点,则当∠A₁M₁N₁=90°时,结论A₁M₁=M₁N₁.是否还成立?

解:小颖认为是成立的,而且由三角形变为正方形,=90°,此时仍可以有(),得到∠1=∠3,这是一道类比探究的题目,所以打算类比第一问的做法,先在上截取(),如图

则,即,从而为等腰直角三角形,这样=135°,从而可以用()证明出≌所以。①∠1+∠2=90°,∠2+∠3=90°;②SAS;③ASA;④括号内应填写的顺序为()

数学课堂上,徐老师出示一道试题:如图所示,在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点.若∠AMN=60°,求证:AM=MN.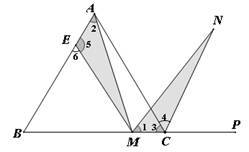

(1)经过思考,小颖展示了一种正确的证明过程.请你将证明过程补充完整.证明:在AB上截取EA=MC,连结EM,得△AEM.
∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB-∠B,       ①       
∴∠1=∠2.
又∵CN平分∠ACP,∠4=∠ACP=60°.
∴∠MCN=∠3+∠4=120°
又∵BA=BC,EA=MC,
∴       ②          ,即BE=BM.
∴△BEM为等边三角形.
∴∠6=60°.∴      ③           
∴∠MCN=∠5.在△AEM和△MCN中,
∵∠1=∠2,AE=MC,∠MCN=∠5.
∴△AEM≌△MCN(ASA).
∴AM=MN.
①∠AMN=∠B=60°;②BA-EA=BC-MC;③∠5=180°-∠6=120°
横线处应填写的顺序为()

在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗?此时,小石思路是这样的:由BM⊥a,CN⊥a得:BM∥CN,又因为a∥BC,∴四边形BMNC为(),又因为∠BMN=90°,∴四边形BMNC为(),因为P是BC的中点,所以可以类比第1、2问倍长中线的方法来证明出PM=PN,也可以证明△PBM≌△PCN()补充以上小石的思路,顺序正确的是()①矩形;②平行四边形;③菱形;④SAS;⑤ASA

在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(2)若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;

图3
小石认为第2问在第1问的基础上旋转了直线a,但P仍为BC的中点,而且BM⊥直线a于点M,CN⊥直线a于点N,认为第1问的方法可以类比到第二问来,所以仍延长MP交NC的延长线于点E,此时可以得到(),所以MP=EP,又因为(),所以NP=ME=MP,理由是()以上括号内要填写的内容顺序为()①△BPM≌△CPE;②△MNE为直角三角形;③直角三角形斜边中线等于斜边一半

在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)延长MP交CN于点E(如图2).求证:①△BPM≌△CPE;②求证:PM=PN;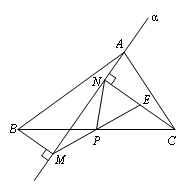

图2
小石的思路是这样的,要证明△BPM≌△CPE,只需找三组条件,首先题干中的点P为BC边中点,可以得到(),然后,题干中BM⊥直线a于点M,CN⊥直线a于点N,所以(),从而∠1=∠2,∠5=∠6,或者加上∠3=∠4,就可以得到△BPM≌△CPE,从而得到(),那么NP就是直角三角形MNE斜边中线,由直角三角形斜边中线等于斜边一半,所以NP=MP。括号里要填写的内容顺序为()①BP=PC;②MP=PE;③BM∥CN

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(3)如图3,若点E是线段AC延长线上的任意一点,其它条件不变.求证:BE=EF.参考小宇同学的作法,第一步应为           ③             .接下来的证明过程如下:∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE,∴BG=CE,又∵CF=AE,∴GE=CF,又∵∠BGE=∠ECF=60°,∴        ④         ,∴BE=EF.③,④处横线上所填内容分别是()

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(2)若点E是线段AC上的任意一点,其它条件不变.如图2,判断线段BE、EF有怎样的数量关系并证明.小宇同学展示出如下正确的作法: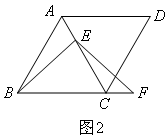解:BE=EF,证明如下:如图2,        ①  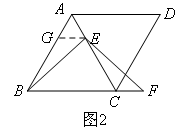      ,∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE,∴BG=CE,又∵CF=AE,∴GE=CF,又∵∠BGE=∠ECF=120°,∴        ②         ,∴BE=EF;①,②处横线上所填内容分别是()

在菱形ABCD中,∠ABC=60°,E是对角线AC上一点.F是线段BC延长线上一点,且CF=AE.连接BE、EF.(1)若点E是线段AC的中点,如图1,则BE与EF的数量关系为BE       EF;

已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(3)如图3,当点D在边CB的延长线上且其他条件不变时,AC、CF、CD之间的等量关系为()

已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF,使∠DAF=60°,连接CF.(2)如图2,当点D在边BC的延长线上且其他条件不变时,AC、CF、CD之间的等量关系为()