2编号:88621题型:单选题测试正确率:0%
问题:如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断
BE,EF,FD之间的数量关系.
(1)发现证明:
小聪把△ABE绕点A逆时针旋转90°至△ADG(如图2),经过推理和计算发现BE,EF,FD之间的数量关系,请判断BE,EF,FD之间的数量关系.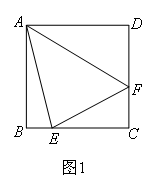

(2)类比引申:
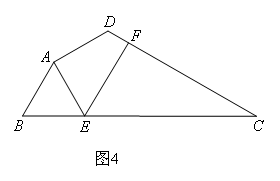
如图3,在四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD?
(3)探究应用:
如图4,在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,
∠ADC=120°,∠BAD=150°,道路BC,CD上分别有景点E,F,且AE⊥AD,![]() 米,现要在E,F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
米,现要在E,F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:![]() ,
,![]() ).
).
(建议学生先打印纸质材料,再做题)
(1)中BE,EF,FD之间的数量关系为( )
5编号:88618题型:单选题测试正确率:0%
(1)类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°,求∠C的度数.
(2)在探究“等对角四边形”性质时,小红画了一个“等对角四边形”ABCD(如图2),其中
∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.由此小红猜想:“对于任意‘等对角四边形’,
当一组邻边相等时,另一组邻边也相等”.
那么小红的发现是正确的吗?猜想是正确的吗?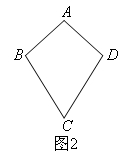
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.
(建议学生先打印纸质材料,再做题)
(1)∠C的度数为( )
10编号:88526题型:单选题测试正确率:0%
(1)问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E,F分别是边BC,CD上的点,
且∠EAF=60°.
求证:EF=BE+DF.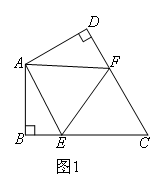
(2)探索延伸:
如图2,在四边形ABCD中,AB=AD,E,F分别是边BC,CD上的点,且![]() ,则当∠B和∠D满足什么条件时,EF=BE+DF成立?
,则当∠B和∠D满足什么条件时,EF=BE+DF成立?
(3)实际应用:
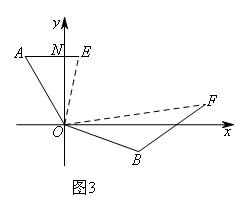
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,则此时两舰艇之间的距离为( )海里.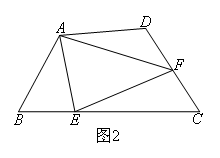
(建议学生先打印纸质材料,再做题)
(1)中证明上述结论的辅助线的作法,有如下说法:①延长FD到G,使DG=BE,连接AG;
②过点A作AG⊥EF于点G;
③将△ABE绕点A逆时针旋转120°得到△ADG(之后证明点G,D,F在同一条直线上).
其中可以证明结论的是( )