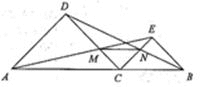
如图，已知C是线段AB上的任意一点（端点除外），分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE，连结AE交CD于点M，连结BD交CE于点N，给出以下三个结论：
①MN∥AB；
② $\frac{1}{MN}=\frac{1}{AC}+\frac{1}{BC}$ ；
③ $MN\leq \frac{1}{4}AB$ ；
其中正确结论的个数是（）

答案

正确答案：D

①△ACD和△BCE为等腰直角三角形，有AD∥CE，CD∥BE；
AD∥CE，则△ADM∽△ECM， $\frac{EM}{AM}=\frac{CE}{AD}$ ;
CD∥BE,则△CDN∽△EBN，有 $\frac{EN}{CN}=\frac{BE}{CD}$
由于AD=CD，BE=CE，
∴ $\frac{EN}{CN}=\frac{EM}{AM}$
∠AEC=∠AEC
∴ $\triangle ACE\sim \triangle MEN$
∴∠EMN=∠EAB
∴MN∥AB，①正确。
② $\frac{CM}{DM}=\frac{CE}{AD}$
∴ $\frac{CM}{CD}=\frac{CE}{AD+CE}$
∴ $CM=\frac{CE\times CD}{AD+CE}$
$\sqrt{2}CM=MN$
$\sqrt{2}AD=\sqrt{2}CD=AC,\sqrt{2}CE=BC$ ,
代入上式有 $MN=\frac{BC*AC}{(AC+BC)}$
即② $\frac{1}{MN}=\frac{1}{AC}+\frac{1}{BC}$

③ $MN=\frac{BC\times AC}{AC+BC}=\frac{AC\times BC}{AB}\leq \frac{1}{4}\times \frac{(AC+BC)^2}{AB}\leq \frac{1}{4}AB$
③正确，答案选D。