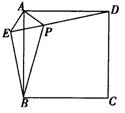
已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，PB＝．下列结论：
①△APD≌△AEB；
②点B到直线AE的距离为2 ；
③EB⊥ED；
④S△APD＋S△APB＝1＋ ；
⑤S正方形ABCD＝4＋ ．
其中正确结论的序号是（       ）

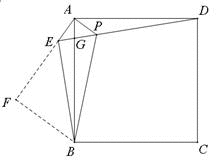
过B做BF⊥AE的延长线于点F
①AE=AP，AB=AD，∠EAB+∠BAP=∠BAP+∠PAD=90°，∴∠BAE=∠DAP
，△AEB≌△APD(SAS)，①正确；
②∠AEB=∠APD=135°，∴∠BEF=45°，AF⊥BF，∴△BEF为等腰直角三角形；
△BEP为直角三角形，,BE=，BF=
∴②错
③∵∠ABE=∠ADE，
∠ADE+∠AGD=90°，∠AGD=∠BGE
∴∠BGE+∠ABE=90°，DE⊥BE，
∴③正确
，④错。
⑤△ABF中，，正方形ABCD的面积=，⑤正确。
故①③⑤正确，答案为D。

略