(2011江苏)如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8 cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2 cm /s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为ts.
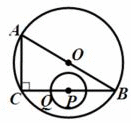
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
(2)已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
答案
(1)直线AB与⊙P相切,
如图,过P作PD⊥AB,垂足为D,
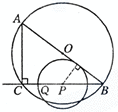
在Rt△ABC中,∠ACB=90°,
∵AB=6cm,BC=8cm,
∴AB=10cm,
∵P为BC中点,
∴PB=4cm,
∵∠PDB=∠ACB=90°,
∠PBD=∠ABC,
∴△PBD∽△ABC,
∴=
,
即=
,
∴PD=2.4(cm),
当t=1.2时,PQ=2t=2.4(cm),
∴PD=PQ,即圆心P到直线AB的距离等于⊙P的半径,
∴直线AB与⊙P相切;
(2)∵∠ACB=90°,
∴AB为△ABC的外接圆的直径,
∴BO= AB=5cm,
连接OP,
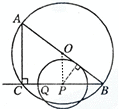
∵P为BC中点,∴PO= AC=3cm,
∵点P在⊙O内部,∴⊙P与⊙O只能内切,
∴5-2t=3,或2t-5=3,
∴t=1或4,
∴⊙P与⊙O相切时,t的值为1或4.
知识点:勾股定理 直线与圆的位置关系 圆与圆的位置关系 相似三角形的判定与性质
(1)根据已知求出AB=10cm,进而得出△PBD∽△ABC,利用相似三角形的性质得出圆心P到直线AB的距离等于⊙P的半径,即可得出直线AB与⊙P相切;
(2)根据BO= AB=5cm,得出⊙P与⊙O只能内切,进而求出⊙P与⊙O相切时,t的值.
对直线与圆的位置关系及圆与圆的位置关系掌握不熟练








