（上接第3，4题）在图3中，D是线段BC延长线上的点，探究DE，DF与BG的关系，你认为正确的是(    )

（上接第3题）在图2中，D是线段BC上的任意一点，DE+DF与BG的关系仍然成立.下列3种思路中你认为可行的是(    )
思路①：连接AD，借助S_△ABD+S_△ACD=S_△ABC；
思路②：过点D作DM⊥BG于点M，然后证明△BMD≌△DEB；
思路③：连接EF，证明EF=BG．

在△ABC中，AB=AC=a，BC=b，且，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F．在图1中，D是BC边上的中点，则DE+DF与BG的数量关系为(    )

（上接第1题）（2）当点E在BA的延长线上时，如图3，点D在BC边上，且CE=DE，按照下面的操作，能够证明AE=BD的是(    )

在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD之间的关系，小明准备分情况进行讨论．
当E是AB中点时，如图1，小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，再由CE=DE可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．但是当E不是AB中点时，就不能照搬上述方式进行证明．此时小明想到了另外一种方式：过点E作EF∥BC，交AC于点F，也能证明AE=BD．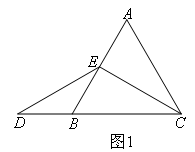

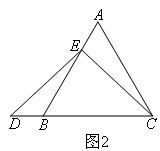
（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要证明一对三角形全等，则证明这对三角形全等不能使用的条件是(    )

（上接第4，5题）实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°
的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进．1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，则此时两舰艇之间的距离为(    )海里．

（上接第4题）探索延伸：
如图2，在四边形ABCD中，AB=AD，E，F分别是边BC，CD上的点，且，则当∠B和∠D满足什么条件时，EF=BE+DF成立？(    )

问题背景：
如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠D=90°．E，F分别是边BC，CD上的点，且
∠EAF=60°．求证：EF=BE+DF．
关于证明上述结论的辅助线的作法，有如下说法：①延长FD到G，使DG=BE，连接AG；②过点A作AG⊥EF于点G；③将△ABE绕点A逆时针旋转120°得到△ADG（之后证明点G，D，F在同一条直线上）．其中可以证明结论的是(    )

（上接第1，2题）（3）若，则n的值是(    )时，MN∥BE．

（上接第1题）（2）若，则的值是(    )