如图,在平面直角坐标系中,四边形ABCD是梯形,AB∥CD,点A,B在x轴上,点D在y轴上,且点B(10,0),C(7,4).直线l经过A,D两点, .动点P在线段AB上从点A出发,以每秒2个单位长度的速度向点B运动,同时动点Q从点B出发,以每秒5个单位长度的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线AD-DC交于点M.设点P,Q运动的时间为t秒(
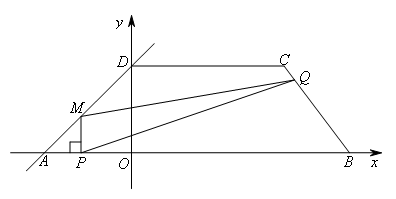
.动点P在线段AB上从点A出发,以每秒2个单位长度的速度向点B运动,同时动点Q从点B出发,以每秒5个单位长度的速度沿B→C→D的方向向点D运动,过点P作PM垂直于x轴,与折线AD-DC交于点M.设点P,Q运动的时间为t秒(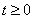 ),
),
△MPQ的面积为S(约定:把线段看成面积为0的三角形).
(1)点A的坐标是( )
- A.
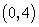
- B.
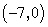
- C.
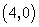
- D.
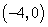
答案
正确答案:D
∵AB∥CD,点A,B在x轴上,点D在y轴上,且点C的坐标为(7,4),
∴点D的坐标为(0,4),
∴OD=4.
∵![]() ,
,
∴OA=OD=4,
∴点A的坐标是(-4,0),故选D.
由于此道题目是动点问题的第一问,首先需要将基本图象研究清楚.
我们已经知道△AOD是等腰直角三角形,腰长为4,
∵点B(10,0),C(7,4)
∴OB=10,DC=7,
如图,过点C作CE⊥x轴于点E,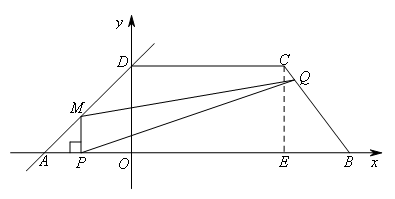
则四边形ODCE是矩形,
∴OE=7,CE=4,
∴BE=3.
在Rt△CEB中,易求BC=5,
∴△CEB是三边关系为3:4:5的直角三角形.
至此,我们将基本图形的特征研究清楚.
略








