学科测评首页 >> 题库 >> 九年级 >> 数学

相关的在线测评卷

动点问题综合测试（二）（通用版）

（上接第2题）（2）S与t之间的函数关系式为( )

A.
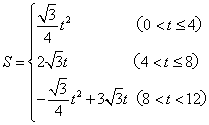
B.
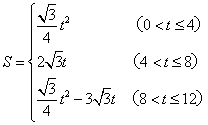
C.
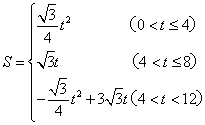
D.

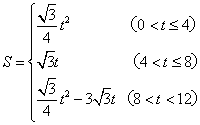
答案

正确答案：C

知识点：等边三角形的判定与性质平行四边形的性质动点问题三角形面积问题

解题思路

当时，点P，Q的位置如图所示，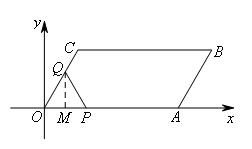

过点Q作QM⊥OA于点M．
由题意得，OP=OQ=t．
在Rt△OQM中，∠QOM=60°，
∴，
∴．
当时，点P，Q的位置如图所示，

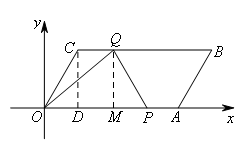
过点Q作QM⊥OA于点M，过点C作CD⊥OA于点D．
在Rt△COD中，∠COD=60°，
∴，
易证，
∴．
当时，点P，Q的位置如图所示，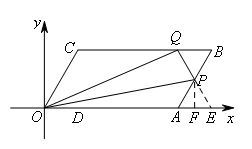

延长QP交x轴于点E，过点P作PF⊥AE于点F．
由题意得，BQ=BP=12-t，∠B=60°，
∴△BPQ为等边三角形．
由BQ∥AE得△BQP∽△AEP，
∴△AEP为等边三角形，
∴OE=OA+AP=t．
易得AP=t-8，
在Rt△APF中，∠PAF=60°，
∴．
∴．
综上得，．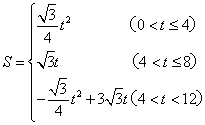

易错点

略

下载次数：0

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>