如图,PD为⊙O的直径,直线BC与⊙O相切于点C,BP的延长线与CD的延长线交于点A,
∠A=28°,∠B=26°,则∠PDC=(    )

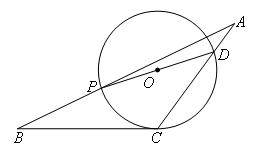
• A.34°
• B.36°
• C.38°
• D.40°

答案

正确答案：B

知识点：切线的性质  

如图，连接OC，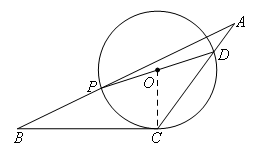

∵BC为⊙O的切线，
∴OC⊥BC，
∴∠OCB=90°．
∵∠A=28°，∠B=26°，
∴∠ACB=126°，
∴∠OCD=36°．
∵OC=OD，
∴∠ODC=∠OCD=36°，
即∠PDC=36°．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>