如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,
点C沿EF折叠后与点O重合,则∠CEF的度数是(    )

1．思路点拨：
①首先结合题目条件，有等腰三角形、角平分线考虑三线合一；
②其次根据OD垂直平分AB，考虑垂直平分线的性质；
③最后，有折叠，要考虑折叠问题的处理思路：先找折痕，折痕两侧的图形是全等图形，进而转移边、转移角，同时，折痕所在直线垂直平分对应点的连线．再利用折叠进行转移和表达；结合条件建等式求解．
2．解题过程：
如图，连接OB．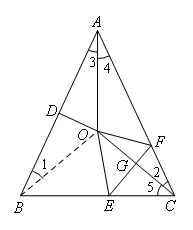

∵AB=AC，AO平分∠BAC，∠BAC=50°
∴∠3=∠4=25°
∵AO=AO
∴△AOB≌△AOC（SAS）
∴∠1=∠2
∵AB=AC，∠BAC=50°
∴∠ACB=∠ABC=65°
∵OD垂直平分AB
∴∠1=∠3=25°
∴∠2=∠1=25°
∴∠5=65°-25°=40°
又由折叠的性质可知：EF⊥OC
∴∠EGC=90°
∴∠CEF=90°-40°=50°，选B
3．易错点：
①对于题目常见的结构不熟悉，不知道等腰三角形和角平分线结合要考虑三线合一，不清楚垂直平分线的性质；
②对于折叠问题，仅仅停留在利用全等转移边和角上，不能利用对称轴垂直平分对应点的连线找互余．

略