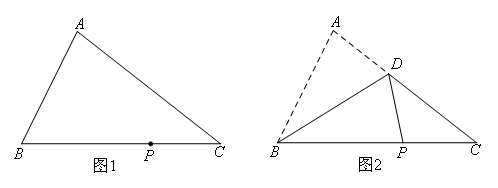
图1为一张三角形纸片ABC,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图2所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为(    )

• A.3:2
• B.5:3
• C.3:5
• D.13:8

答案

正确答案：A

知识点：转化法(等底或等高)求面积  折叠问题  

1．思路点拨：
①已知面积求线段之间的比值，往往考虑借助等底（等高）模型转移面积．
②折叠变换是全等变换，全等三角形面积相等．
2．解题过程：
解：由题意可得：
由折叠性质可知，△ABD≌△PBD
∴
∴
∴BP:PC==30:20=3:2．
故选A．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>