在△ABC中,∠C=90°,AC=3,BC=4,O是AB上的一点,且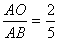 ,点P是AC上的一个动点,
,点P是AC上的一个动点, 交线段BC于点Q(不与点B,C重合).若AP=2,则CQ的长为( )
交线段BC于点Q(不与点B,C重合).若AP=2,则CQ的长为( )

- A.
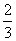
- B.
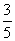
- C.
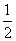
- D.2
答案
正确答案:C
知识点:相似三角形的判定与性质 三等角模型
考虑∠C和∠QPO都是直角,过点O作AC的垂线,构造直角,利用三等角模型解题.
如图,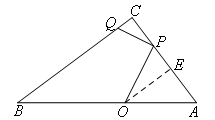
过点O作OE⊥AC,垂足为点E.
在Rt△ABC中,∵AC=3,BC=4,
∴AB=5.
∵![]() ,
,
∴AO=2.
易证△OEA∽△BCA,即△OEA是三边之比为3:4:5的直角三角形,
∴![]() ,
,![]() .
.
∵AP=2,AC=3,
∴PC=1,![]() .
.
∵∠C=∠PEO,∠CPQ=∠EOP=90°-∠OPE,
∴△CPQ∽△EOP,
∴![]() ,即
,即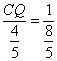 ,
,
∴![]() .
.
略








