如图，在平面直角坐标系中，点A（0，6），点B是x轴上的一个动点，连结AB，取AB的中点M，将线段MB绕着点B按顺时针方向旋转90°，得到线段BC．过点B作x轴的垂线交直线AC于点D．设点B坐标是（t，0）．（1）当t＝4时，求直线AB的解析式；（2）当t＞0时，用含t的代数式表示点C的坐标及△ABC的面积；（3）是否存在点B，使△ABD为等腰三角形？若存在，请求出所有符合条件的点B的坐标；若不存在，请说明理由．

答案

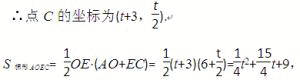
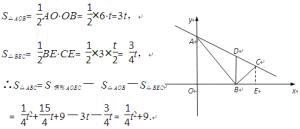
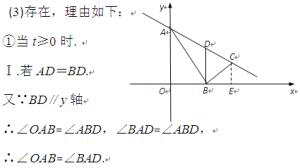
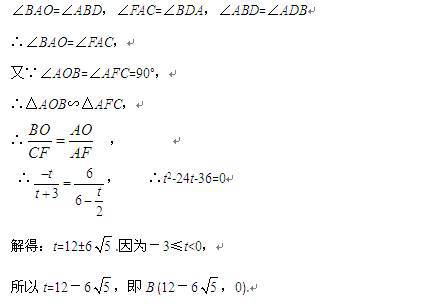
③当t<－3时，如图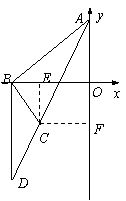，∠ABD是钝角.
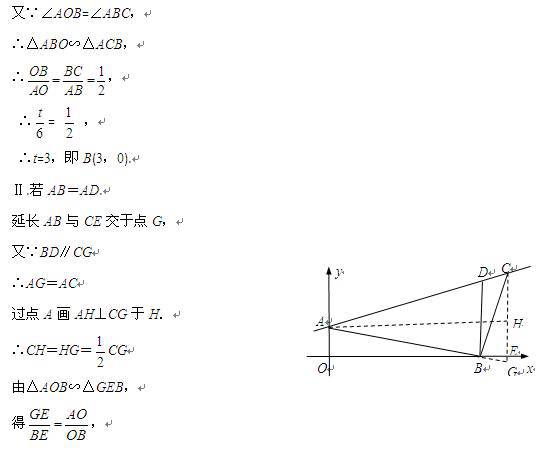
设AB=BD，过点C分别作CE⊥x轴，CF⊥y轴于点E，点F，
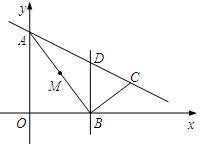
可求得点C的坐标为(t+3，)，
∴CF=－(t+3)，AF=6－，
∵AB=BD，
∴∠D=∠BAD.
又∵BD∥y轴，
∴∠D=∠CAF，
∴∠BAC=∠CAF.
又∵∠ABC=∠AFC=90°，AC=AC，
∴△ABC≌△AFC，
∴AF＝AB，CF=BC，
∴AF=2CF，即6－=－2(t+3)，
解得：t=－8，即B(－8，0).
综上所述，存在点B使△ABD为等腰三角形，
此时点B坐标为：B₁(3，0)，B₂(12＋6，0)，B₃(12－6，0)，B₄(－8，0).