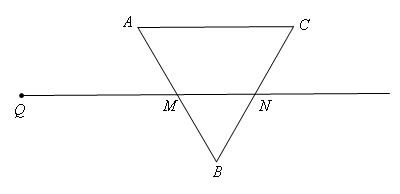
如图,射线QN与等边三角形ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,
QM=4cm.动点P从点Q出发,沿射线QN以1cm/s的速度向右移动,经过ts,以点P为圆心,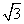cm为半径的圆
与△ABC的边相切(切点在边上),则t可取的一切值为( )

A.t=2,4,6,8
B.t=2,3,4,5,6,7,8
C.t=2或4≤t≤6或t=8
D.t=2或3≤t≤7或t=8

答案

正确答案：D

分为三种情况：
①如图1，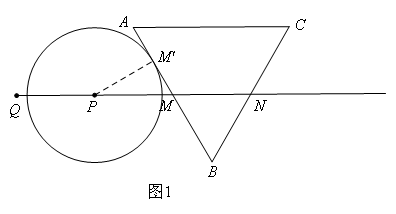

当⊙P与AB相切于点时，连接，
则cm，PM=2cm，
∴QP=4-2=2cm，即t=2．
②如图2，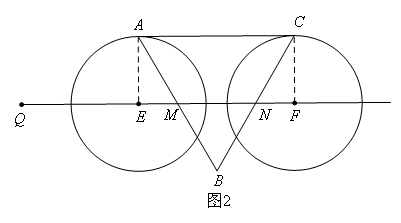

过A作AE⊥QN于点E，过C作CF⊥QN于点F，
∵AC∥QN，且易求得AC与QN之间的距离为
∴点P在线段EF上运动时始终与边AC相切，
又∵QE=3cm，QF=7cm，
∴当3≤t≤7时，⊙P与边AC相切．
③如图3，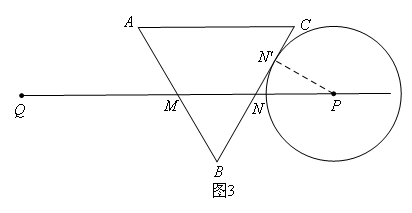

当⊙P与BC相切于点时，连接，
则，
∴QP=4+2+2=8cm，
即t=8．
故选D．