在边长为8的正方形ABCD中,点E是BC边上一点,且BE=6.点H是正方形ABCD边上的一点,连接BH,交线段AE于点F,若BH=AE,则线段FH的长为(    )

题中没有说明点H在正方形ABCD的哪条边上，需进行分类讨论．
①如图1，点H在边CD上，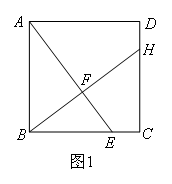

∵四边形ABCD是正方形，
∴AB=BC，∠ABC=∠BCH=90°，
又∵BH=AE，
∴Rt△ABE≌Rt△BCH，
∴∠AEB=∠BHC．
∵∠EBF=∠HBC，
∴△BEF∽△BHC，
∴．
在Rt△ABE中，，
∴BH=10，
∴，
解得BF=4.8，
∴FH=BH-BF=10-4.8=5.2．
②如图2，点H在边AD上，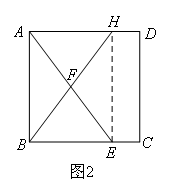

连接EH，
可证得Rt△ABE≌Rt△BAH，四边形ABEH是矩形，
∴AH=BE=6，AE=BH=10，
∴．
综上，线段FH的长是5.2或5．

略