（8分）如图：正方形OABC中，B点的坐标为（2，2）．D、E分别在边AB、BC上，F在BC的延长线上．且AD=CF，∠EDO=∠DOC．（1）猜想△OAD与△OCF能否通过旋转重合？请证明你的猜想．（2）若D是AB的中点．求直线DE的解析式．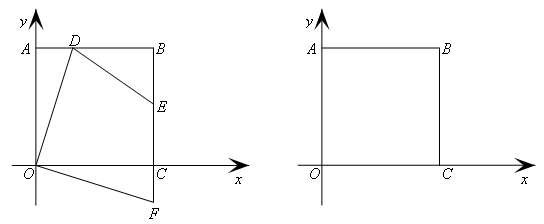
答案
解：（1）△OAD与△OCF能通过旋转重合；
证明：在Rt△OAD和Rt△OCF中
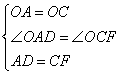
∴△OAD≌△OCF(SAS)
∴OAD绕点O顺时针旋转90°与△OCF重合．
（2）
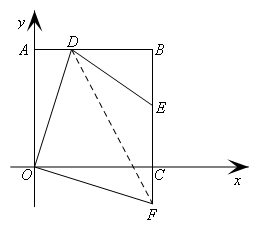
如图，连接DF
∵D是AB的中点，
∴D（1，2），AD=DB=1，
设CE=x，则EF=EC+CF=EC+AD=x+1，BE=2-x
∵∠OFC=∠ODA=∠DOC=∠ODE，OD=OF
∴∠ODF=∠OFD
∴∠EDF=∠EFD
∴DE=EF=x+1在Rt△BDE中，
∴
解得：x=
∴E（2，）
设DE的解析式为：y=kx+b
则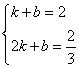
解得：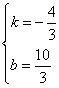
∴直线DE的解析式为：
知识点：坐标与图形变化-旋转 正方形性质
略
略
WORD格式（
