（8分）如图，四边形ABCD是矩形，对角线AC、BD相交于点O，BE∥AC交DC的延长线于点E．（1）求证：BD=BE；（2）若∠DBC=30°，BO=4，求四边形ABED的面积．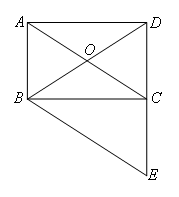
答案
（1）证明：∵四边形ABCD是矩形
∴AC=BD，AB∥CD
∵BE∥AC
∴四边形ABEC是平行四边形
∴AC=BE
∴BD=BE
（2）解：∵在矩形ABCD中，BO=4，
∴BD=2BO=2×4=8，
∵∠DBC=30°，
∴CD=
BD=×8=4
∴AB=CD=4，DE=CD+CE=CD+AB=8，
在Rt△BCD中，
∵∠DBC=30°，DC=4
∴BC=
∴四边形ABED的面积=×（4+8）×=
知识点：含30度角的直角三角形 矩形的性质与计算
略
略
WORD格式（
