图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作平行四边形APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0°<α<90°).(1)求证:∠EAP=∠EPA;(2)平行四边形APCD是否为矩形?请说明理由;(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.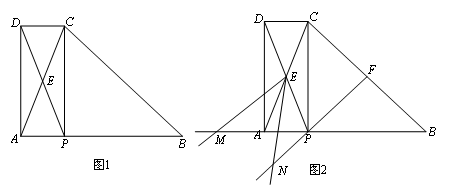
答案
(1)证明:在ΔABC和ΔAEP中
∵∠ABC=∠AEP,∠BAC=∠EAP
∴∠ACB=∠APE在ΔABC中,AB=BC
∴∠ACB=∠BAC
∴∠EPA=∠EAP
(2)平行四边形APCD是矩形,理由如下:
∵四边形APCD是平行四边形
∴AC=2EA, PD=2EP
∵由(1)知∠EPA=∠EAP
∴EA=EP则AC=PD
∴平行四边形APCD是矩形
(3)EM=EN
∵EA=EP
∴ ∠EPA=90°-α
∴∠EAM=180°-∠EPA=180°-(90°-α)=90°+α
由(2)知∠CPB=90°,F是BC的中点,
∴FP=FB
∴∠FPB=∠ABC=α
∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°-α+α=90°+α
∴∠EAM=∠EPN
∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN
∴∠AEP=∠MEN
∴∠AEP-∠AEN=∠MEN-∠AEN即∠MEA=∠NEP
∴ΔEAM≌ΔEPN
∴ EM=EN
知识点:全等三角形的判定 等腰三角形的性质 平行四边形的性质 矩形的判定 旋转的性质
略
略








