如图，在梯形ABCD中，AD∥BC，E是BC的中点，AD=5，BC=12，CD=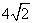，∠C=45°，点P是BC边上一动点，设PB的长为x．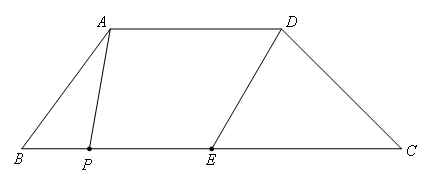
（1）当x的值为       时，以点P、A、D、E为顶点的四边形为直角梯形；
（2）当x的值为       时，以点P、A、D、E为顶点的四边形为平行四边形；
（3）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？试说明理由．

答案

解：（1）3或8；
（2）1或11；
（3）由（2）知，当BP=11时，以点P、A、D、E为顶点的四边形是平行四边形.
∴EP=AD=5过点D作DF⊥BC于F，则DF=FC=4，
∴FP=3
∴DP===5
∴EP=DP，故此时四边形PDAE是菱形即以点P、A、D、E为顶点的四边形能构成菱形

知识点：平行四边形的判定  菱形的判定  梯形  

略

略

下载次数：3

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>