如图1，在正方形ABCD中，等腰直角三角形BEF的直角顶点E在BC边上，连结DF，取DF的中点M，连结ME、MC.
（1）判断ME、MC的关系并给出证明．
（2） 如果将△BEF逆时针旋转一定角度（在0°到45°之间），如图2，则ME、MC是否保持同样的关系？证明你的结论．

答案

（1）EG=CG且EG⊥CG
证明：如图，延长EM交CD于点N．


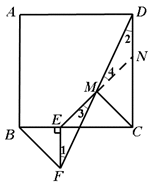
∵BE⊥EF，且BE⊥CD∴EF∥CD，∴∠1=∠2．
又∵∠3=∠4，FM=DM，
∴△FEM≌△DNM，
∴EF=DN，EM=MN．
∵△BEF为等腰直角三角形，
∴BE=EF，∴BE=DH．
∵CD=BC，∴CE=CN．
∴△ECN为等腰直角三角形．
又∵EM=MN，
∴EG=CG且EG⊥CG．
（2）仍然成立．
证明如下：如图，延长CM至N，使MN=CM，连接NF，EN、EC．

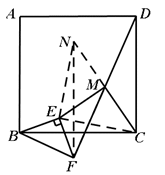
∵MF=MD，∠NMF=∠CMD，MN=CM，
∴△NFM≌△CDM，
∴NF=CD，∠MNF=∠MCD，
∴NF∥CD．
∵正方形ABCD，
∴BC=DC,BC⊥DC,
∴NF=BC，NF⊥BC．
∵△BEF是等腰直角三角形，
∴BE=EF，∠EBC=∠NFE，
∴△BEC≌△FEN，
∴NE=EC，∠BEC=∠FEN，
∴∠BEF=∠NEC=90°，
∴△ECN为等腰直角三角形．
又∵CM=MN，
∴EM=CM且EM⊥CM．

知识点：旋转的性质  

<<上一题   下一题>>