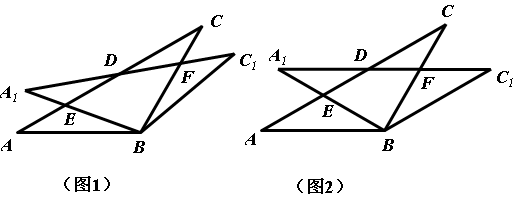
在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A₁BC₁ ， A₁B交AC于点E， A₁C₁分别交AC、BC于D、F两点．
（1）如图1，观察并猜想，在旋转过程中，线段EA₁与FC有怎样的数量关系？并证明你的结论；
（2）如图2，当α=30°时，试判断四边形BC₁DA的形状，并说明理由；
（3）在（2）的情况下，求ED的长．

答案

解：（1）EA₁=FC
（2）四边形BC₁DA为菱形
（3）ED= $2-\frac{2\sqrt{3}}{3}$

解：（1）EA₁=FC
证明：在△A₁BF和△CBE中，
$\begin{cases} \angle A_{1}=\angle C\\ A_{1}B=BC \\ \angle A_{1}BC= \angle A_{1}BC \end{cases}$
∴△A₁BF≌△CBE（ASA）
∴A₁E=CF
（2）∵∠A₁=∠ABA₁，∠C=∠CBC₁
∴AB∥C₁D，AD∥BC₁
∴四边形BC₁DA为平行四边形
又∵AB=BC₁
∴四边形BC₁DA为菱形
（3）如图，过点E做EG⊥AB于点G

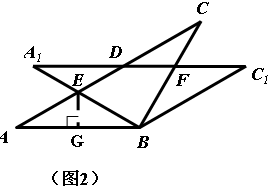
∵∠A=∠ABA₁=30°
∴△ABE为等腰三角形
∴AG=GB=1
∴AE= $\frac{2\sqrt{3}}{3}$
由（2）证得四边形BC₁DA为菱形
∴AD=AB=2
∴ED=AD-AE=2- $\frac{2\sqrt{3}}{3}$

ED的长

下载次数：1

WORD格式（含答案版下载无答案版下载）

<<上一题下一题>>