 的半径为2,点A、B、C在
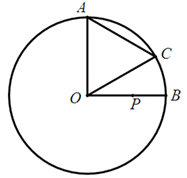
的半径为2,点A、B、C在 上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值.
上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值.
答案
作A关于OB的对称点,连接
C,交OB于P,PA+PC的最小即为
C的长,∵∠AOC=60°,△AOC是等边三角形,所以CD=
OC=
×2=
,∴∠
OC=120°,OC=O
,∠A
C=∠OC
=30°,在Rt△D
C中,
C=2CD=2
,
C=2

知识点:轴对称-最短路线问题
作A关于OB的对称点,连接
C,交OB于P,PA+PC的最小即为
C的长,∵∠AOC=60°,△AOC是等边三角形,所以CD=
OC=
×2=
,∴∠
OC=120°,OC=O
,∠A
C=∠OC
=30°,在Rt△D
C中,
C=2CD=2
,
C=2

没有思路








