如图,△ABC中,∠ACB=2∠B,BC=2AC.求证:∠A=90°

答案
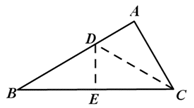
作BC的垂直平分线,与AB交于点D,与BC交于点E,连接CD,则:DB = DC ,∴∠B = ∠DCB,∴∠ACB= 2∠B = 2∠DCB,又∵∠ACB=∠DCB+∠ACD,∴∠DCB=∠ACD,又∵BE=CE=BC,∵BC = 2AC,EC=AC,∠ACD=∠ECD,DC=DC,∴△ACD≌△ECD(ASA),∠DAC=∠DEC,∠DEC=90°,所以∠DAC=90°即∠A=90°
知识点:线段垂直平分线的性质 等腰三角形的性质
作BC的垂直平分线,与AB交于点D,与BC交于点E,连接CD,则:DB = DC ,∴∠B = ∠DCB,∴∠ACB= 2∠B = 2∠DCB,又∵∠ACB=∠DCB+∠ACD,∴∠DCB=∠ACD,又∵BE=CE=BC,∵BC = 2AC,EC=AC,∠ACD=∠ECD,DC=DC,∴△ACD≌△ECD(ASA),∠DAC=∠DEC,∠DEC=90°,所以∠DAC=90°即∠A=90°

知识掌握不牢,没有思路








