在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E，求证：DE=AD+BE．小强在做这道题目的时候部分分析思路如下：从图中知道DE=CD+CE，只需证明AD=CE，BE=CD即证明△ACD≌△CBE,题中已知AC=CB，AD⊥MN，BE⊥CE，采取的判定方法是AAS，此时需要找的第三组条件 = .因为AD⊥MN，所以 ，而∠ACB=90°，即 ，所以第三组条件就得以证出.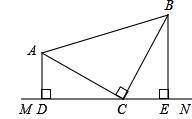
①∠ACD+∠DAC=90°
②∠ACB=∠CEB
③∠ACD+∠BCE=90°
④∠DAC=∠ECB
- A.④①②
- B.②①③
- C.②④①
- D.④①③
答案
正确答案：D
知识点：一组条件不好找
略
略
WORD格式（
