由10个小立方体搭成的几何体的俯视图如图所示，小正方形中的数字表示在该位置的小立方体的个数，请画出这个几何体的主视图和左视图．

由6个小立方体搭成的几何体的俯视图如图所示，小正方形中的数字表示在该位置的小立方体的个数，请画出这个几何体的主视图和左视图．

如图所示是一个用7个小立方体搭成的几何体，请画出它的三视图．

如图所示是一个用5个小立方体搭成的几何体，请画出它的三视图．

用正方体小木块搭建成的几何体，下面三个图分别是它的主视图、俯视图和左视图，请你观察它是由多少块小木块组成的．
 

将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为8cm，宽为6cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？

若要使得图中平面展开图折叠成正方体后，相对面上的两个数之和为10，求x+y+z的值．

在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．
（1）在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；
（2）当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE＋DF与CG之间满足的数量关系，然后证明你的猜想；
（3）当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）

数学课上，李老师出示了如下框中的题目．

小敏与同桌小聪讨论后，进行了如下解答：
(1)特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系．请你直接写出结论：AE＿＿DB（填“＞”、“＜”或“=”）
(2)特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE＿＿DB（填“＞”、“＜”或“=”）．理由如下：如图2，过点E作EF//BC,交AC于点F，（请你完成以下解答过程）

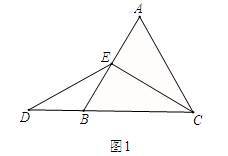
(3)拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）．

数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角的平分线CF于点F，求证：AE=EF．
经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以．
在此基础上，同学们作了进一步的研究：
（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；
（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．