1编号:136711题型:解答题测试正确率:0%
2编号:136707题型:解答题测试正确率:0%
3编号:136704题型:填空题测试正确率:0%
4编号:136695题型:单选题测试正确率:0%
5编号:136688题型:解答题测试正确率:0%
在△ABC中,AC=BC,CD是AB边上的高.
问题发现:
(1)如图1,若∠ACB=90°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转90°,得到线段CF,连接BF,我们会发现CD,BE,BF之间的数量关系是CD=![]() (BE+BF),请你证明这个结论;
(BE+BF),请你证明这个结论;
提出猜想:
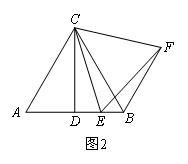
(2)如图2,若∠ACB=60°,点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转60°,得到线段CF,连接BF,猜想线段CD,BE,BF之间的数量关系是 ;
拓广探索:
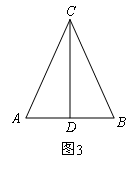
(3)若∠ACB=α,CD=k·AB(k为常数),点E是线段AB上一个动点(点E不与点A,B重合),连接CE,将线段CE绕点C逆时针旋转α,得到线段CF,连接BF.请你利用上述条件,根据前面的解答过程得出类似的猜想,并在图3中画出图形,标明字母,不必解答.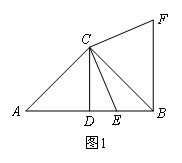
6编号:136683题型:解答题测试正确率:0%
8编号:136676题型:单选题测试正确率:0%
9编号:136675题型:单选题测试正确率:0%
10编号:136067题型:解答题测试正确率:0%