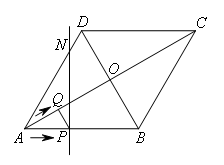
如图，菱形ABCD的边长为20cm，∠ABC=120°．动点P，Q同时从点A出发，其中P以4cm/s的速度，沿A→B→C的路线向点C运动；Q以cm/s的速度，沿A→C的路线向点C运动．当P，Q到达终点C时，整个运动随之结束，设运动时间为t（秒）．
（1）在点P，Q运动过程中，请判断PQ与对角线AC的位置关系，并说明理由．
（2）若点Q关于菱形ABCD的对角线交点O的对称点为M，过点P且垂直于AB的直线l交菱形ABCD的边AD（或CD）于点N．
①当t为何值时，点P，M，N在同一直线上？
②当点P，M，N不在同一直线上时，是否存在这样的t，使得△PMN是以PN为一直角边的直角三角形？若存在，请求出所有符合条件的t值；若不存在，请说明理由．

如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P从O点出发沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t（秒）．将线段BP的中点绕点P按顺时针方向旋转60°得到点C，点C随点P的运动而运动，连接CP，CA，过点P作PD⊥OB于点D。
（1）填空：PD的长为       （用含t的代数式表示）．
（2）求点C的坐标（用含t的代数式表示）．
（3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求出t的值；若不能，请说明理由．

如图1，在四边形ABCD中，∠D=90°，BC∥AD，BC=20，DC=16，AD=30．动点P从点D出发，沿射线DA方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动时间为t（秒）．
（1）设△BPQ的面积为S，求S与t之间的函数关系式．
（2）当t为何值时，使得线段PQ与线段AB相交于点O，且2AO=OB？
（3）当t为何值时，使得PQ⊥BD？
（4）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

如图，在△ABC中，ABC=90°，AB=6，BC=8，动点P从点A出发，沿AC向点C移动．同时，动点Q从点C出发，沿CB向点B移动．在运动过程中，始终满足AP=2CQ，当其中有一点到达终点时，它们都停止移动．设CQ=x．
（1）求△CPQ的面积S关于x的函数解析式；
（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出x的值．

如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB₁∥AC．动点D从点A出发沿射线AC方向运动，同时动点E从点C出发沿射线AC方向运动．过点D作DH⊥AB于点H，过点E作EF⊥AC，交射线BB₁于点F，G是EF的中点，连接DG．设AD=5a，CE=3a．
（1）当a为何值时，AD=AB，并求出此时DE的长；
（2）当△DEG与△ACB相似时，求a的值．

如图，矩形OABC在平面直角坐标系中，若OA=2，OC=．
（1）求B，C两点的坐标；
（2）把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求
直线BB′的解析式；
（3）在直线BB′上是否存在点P，使△ADP为直角三角形？若存在，请求出
点P的坐标；若不存在，请说明理由．

如图，在Rt△ABC中，ACB=90°，AC=6，BC=8，点D在边AB上运动，DE平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．
（1）当AD=CD时，求证：DE∥AC．
（2）探究：是否存在这样的AD，使得△BME与△CNE相似？

如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿着AB向点B运动；同时点Q从点C出发，沿CA向点A运动，当点P到达点B时，点Q随之停止运动．已知．
（1）当AP为何值时，PQ∥BC？
（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能，说明理由．

大量时间被我花在了练习说英语上。

教室应该每天被学生打扫。