已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，∠E=∠1．
求证：AD平分∠BAC．

证明：如图，

                             
∴∠E=      （两直线平行，同位角相等）
∠1=      （两直线平行，内错角相等）
∵∠E=∠1（已知）
∴∠2=∠3（等量代换）
∴AD平分∠BAC（角平分线的定义）
①

②

③∠2；④∠3．
以上空缺处依次所填正确的是(    )

已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，∠E=∠1．
求证：AD平分∠BAC．


①
；
②
；③∠2；④∠3．
以上空缺处依次所填正确的是(    )

已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，若AD平分∠BAC，求证：∠BFG=∠E．

证明：如图，

∵AD⊥BC，EG⊥BC（已知）
                                 
∵AD平分∠BAC（已知）
∴∠1=∠2（角平分线的定义）
∴∠BFG=∠E（等量代换）
横线处应填写的过程，顺序正确的是(    )
①∴AD∥EG（两直线平行，同位角相等）
②∴AD∥EG（同位角相等，两直线平行）
③∴∠1=∠BFG，∠2=∠E（两直线平行，同位角相等）
④∴∠ADC=∠EGC=90°（垂直的定义）

已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，
∠E=∠1．求证：AD平分∠BAC．

证明：如图，

                             
∴∠E=      （两直线平行，同位角相等）
  ∠1=      （两直线平行，内错角相等）
∵∠E=∠1（已知）
∴∠2=∠3（等量代换）
∴AD平分∠BAC（角平分线的定义）
①

②

③∠2；④∠3．
以上空缺处依次所填正确的是(    )

如图，在△ABC中，∠B=∠C，FD⊥BC于点D，DE⊥AB于点E，∠AFD=158°，求∠EDF的度数．

解：如图，

                         
∴∠1+∠B=90°
  ∠2+∠C=90°（直角三角形两锐角互余）
∵∠B=∠C（已知）
∴∠1=∠2（同角或等角的余角相等）
∵∠AFD=158°（已知）
∴∠2=180°-∠AFD
     =180°-158°
     =22°（平角的定义）
∴∠1=22°（等量代换）
                         
以上空缺处依次所填最恰当的为(    )
①

②

③

④

已知：如图，在△ABC中，AD⊥BC于点D，E是CA延长线上一点，EG⊥BC于点G，若AD平分∠BAC，求证：∠BFG=∠E．

解：如图，

∵AD⊥BC，EG⊥BC（已知）
                        
∵AD平分∠BAC（已知）
∴∠1=∠2（角平分线的定义）
∴∠BFG=∠E（等量代换）
横线处应填写的过程最恰当的是(    )
①∴AD∥EG（两直线平行，同位角相等）
②∴AD∥EG（同位角相等，两直线平行）
③∴∠1=∠BFG，∠2=∠E（两直线平行，同位角相等）
④∴∠ADC=∠EGC=90°（垂直的性质）

已知：如图，在Rt△ACB中，∠ACB=90°，CD⊥AB于点D，E为AC上一点，G为BC上一点，GF⊥AB于点F，∠1+∠2=180°．求证：DE⊥AC．

证明：如图，
∵CD⊥AB，GF⊥AB（已知）
∴∠GFB=∠CDB=90°（垂直的定义）
∴CD∥GF（同位角相等，两直线平行）
∴∠3+∠2=180°（两直线平行，同旁内角互补）
∵∠1+∠2=180°（已知）
∴∠1=∠3（同角或等角的补角相等）
                    
∴∠AED=90°（等量代换）
∴DE⊥AC（垂直的定义）
横线处应填写的过程最恰当的是(    )

已知：如图，在△ABC中，∠BAC=50°，∠ABC=60°，AD⊥BC，BE⊥AC，垂足分别为D，E，AD，BE相交于点H，求∠AHB的度数．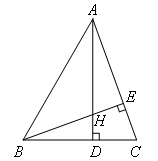

解：如图，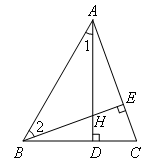

∵AD⊥BC（已知）
∴∠ADB=90°（垂直的性质）
∵∠ABC=60°（已知）
∴∠1=90°-∠ABC
     =90°-60°
     =30°（直角三角形两锐角互余）
                               
∴∠AHB=180°-∠1-∠2
       =180°-30°-40°
       =110°（三角形的内角和是180°）
横线处应填写的过程，顺序正确的是(    )
①∵BE⊥AC（已知）
②∵AD⊥BC（已知）
③∵∠BAC=50°（已知）
④∴∠2=90°-∠BAC
       =90°-50°
       =40°（直角三角形两锐角互余）
⑤∴∠BEA=90°（垂直的性质）
⑥∴∠ADB=90°（垂直的性质）

已知：如图，在△ABC中，∠BAC=50°，∠ABC=60°，AD⊥BC，BE⊥AC，
垂足分别为D，E，AD，BE相交于点H，求∠AHB的度数．

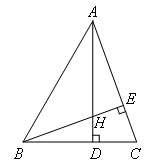
解：如图，

                           
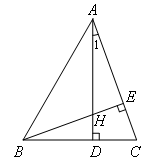
∵BE⊥AC（已知）
∴∠AEH=90°（垂直的性质）
∵∠AHB是△AHE的一个外角（外角的定义）
∴∠AHB=∠1+∠AEH
       =20°+90°
       =110°（三角形的一个外角等于和它不相邻的两个内角的和）
横线处应填写的过程，顺序正确的是(    )
①∵∠BAC=50°，∠ABC=60°（已知）
②∵AD⊥BC（已知）
③∴∠ADC=90°（垂直的性质）
④∴∠C=180°-∠BAC-∠ABC
       =180°-50°-60°
       =70°（三角形的内角和是180°）
⑤∴∠1=90°-∠C
       =90°-70°
       =20°（直角三角形两锐角互余）

如图，在△ABC中，∠B=∠C，D为CA延长线上一点，DF⊥BC于点F，交AB于点E．求证：∠D=∠AED．

证明：如图，

∵DF⊥BC（已知）
                           
∵∠1=∠2（对顶角相等）
∴∠1=∠D（等量代换）
即∠D=∠AED
横线处应填写的过程，顺序正确的是(    )
①∵∠B=∠C（已知）
②∵∠1=∠2（对顶角相等）
③∴∠D+∠C=90°，∠2+∠B=90°（直角三角形两锐角互余）
④∴∠2=∠D（等角的余角相等）
⑤∴∠EFB=∠DFC=90°（垂直的性质）