如图，点E是平行四边形ABCD内一点，DE⊥AD，∠CBE=∠CDE，∠BCE=45°，CE的延长线交AD于点F，连接BF．下列结论：①BE⊥AB；②BE=CD；③AF=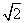CE，其中正确的是(    )

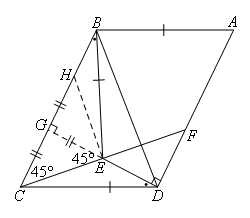
①如图，平行四边形中对角相等，因而∠CBA=∠CDA，
而∠CBE=∠CDE，因此∠ABE=∠EDF=90°，故①对．
②延长DE交BC于点G，则∠DGC=90°，
由∠BCE=45°，可得等腰Rt△GCE，因而GC=GE，
结合∠CBE=∠CDE，∠DGC=∠BGE，
可证△BGE≌△DGC（AAS）因此BE=DC，故②对．
③过点E作EH⊥CE交BC于点H．
可得等腰Rt△CEH，则CH=CE，EH=CE，
接下来，需要证明：CH=AF，即BH=DF，
只需证明BH=DE即可，由∠BHE=∠DEC=135°，
可证△BEH≌△DCE（AAS），因而BH=DE，
故BH=DF，CH=AF，AF=CE，故③对．
综上，①②③对，故选D

略