已知四边形ABCD的两条对角线AC与BD互相垂直，则下列结论正确的是(    )

选项A：由AC⊥BD，AC=BD，只能得到四边形的对角线互相垂直且相等，不能得到对角线互相平分，故不一定是菱形，选项A错误．
选项B：当AC垂直平分BD时，AB=AD，CB=CD成立，但此时四边形ABCD不一定为菱形，如图，

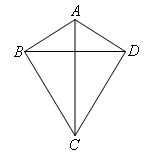
∴选项B错误．
选项C：当AB=AD=BC时，四边形ABCD是菱形，说法正确，理由如下：
如图，

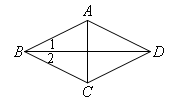
∵AB=BC，BD⊥AC，
易得∠1=∠2，
∴△ABD≌△CBD(SAS)，
∴CD=AD，
∴AB=AD=BC=CD，
∴四边形ABCD是菱形．
选项D：当AC垂直平分BD且AC=BD时，同样满足AC=BD，AD=AB，但此时四边形ABCD不为正方形，如图，

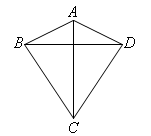
∴选项D错误．

略