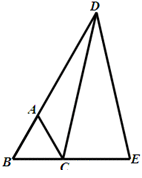
等边三角形ABC,延长BA至D,延长BC至E,使AD=BE.根据以上条件,你能判断CD与DE之 间
的关系吗?请给予证明.
答案
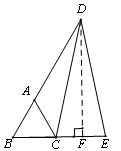
过点D作BE所在直线的垂线,垂足为F
设等边△ABC的边长为m,CE=n.
则BE=BC+CE=m+n
∵AD=BE,∴BD=BA+AD=m+(m+n)=2m+n
∵△DFB为直角三角形,且∠B=60°
∴∠BDF=30°,∴ BF= = m+
∴CF=BF-BC= m+-m=
,∴CF=FE
即F为CE的中点 ,又∵DF⊥CE
∴DF为线段CE的垂直平分线,∴CD=DE.
知识点:线段垂直平分线的性质
可判断CD与DE之间的关系为相等,过点D作BE所在直线的垂线,垂足为F,可设等边△ABC的边长为m,CE=n.则可将BE表示出来为m+n,有已知条件AD=BE可知,BD=2m+n,在直角三角形DFB中,∠B=60°,可得∠BDF=30°,进而可将边BF表示出来,就是(2m+n)/2,因此可得CF=n/2,可得F为CE的中点 ,再根据DF⊥CE可知DF为线段CE的垂直平分线,所以CD=DE
略








