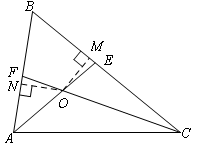
如图,在△ABC中,∠B=60°,∠A、∠C的角平分线AE、CF相交于点O.
求证:OE=OF.

答案
分别向边AB、BC作垂线,垂足为N、M.
则ON=OM,∵∠B=60°,∴∠BAC+∠BCA=120°
又AE、CF是∠A、∠C的角平分线,所以∠OAC+∠OCA=60°,
∴∠AOC=120°,即∠FOE=120°,
在四边形BNOM中,∵∠B=60°,∴∠NOM=120°
∴∠NOF=∠MOE,∴Rt△NOF≌Rt△MOE,∴OE=OF.
知识点:全等三角形的判定
分别向边AB、BC作垂线,垂足为N、M.根据角平分线的性质知,ON=OM,有∠B=60°知∠BAC+∠BCA=120°,又因为AE、CF是∠A、∠C的角平分线,所以∠OAC+∠OCA=60°,可得∠AOC=120°,即∠FOE=120°,因此在四边形BNOM中,由已知条件∠B=60°可知∠NOM=120°,因此可证Rt△NOF≌Rt△MOE,结论得证。
找合适的辅助线,直角三角形全等的判定








